
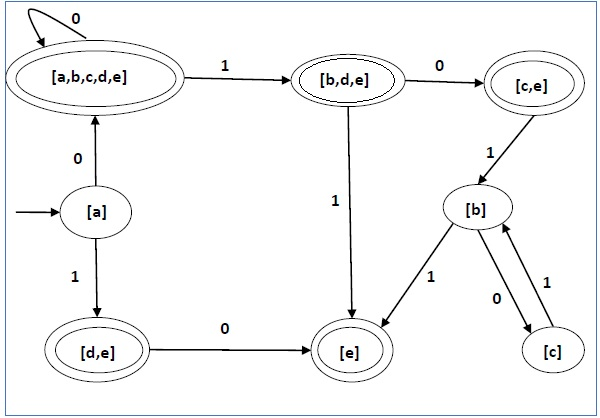
Design a DFA to recognize strings with an equal number of strings '01' and '10'. Design a DFA to recognize strings with an equal number of ones and zeros. Nondeterministic Finite Automata 0 start A NFA that recognizes the strings “and”, & “any” n 1 2 3 4 5 6 d n y a aĮxamples Design a DFA to recognize strings that start out with k zeros followed by k ones. Even Odd 0 0 1 1 StartĭFA Examples Strings containing the substring 001 '001' 0 0 1 1 '0' '00' 0 1 0,1įinite State Machine (DFA) 0 1 2 3 4 start h e 5 6 8 9 7 ACCEPTED State Machine that recognizes the strings “ he”, “hers”, “his”, and “she”įinite State Machine (DFA) State Machine that recognizes the strings “ he”, “hers”, “his”, and “she” 0 1 2 3 4 start h e 5 6 8 9 7 ACCEPTED r sįinite State Machine (DFA) 0 1 2 3 4 start h 5 6 8 9 7 ACCEPTED i s State Machine that recognizes the strings “ he”, “hers”, “his”, and “she”įinite State Machine (DFA) 0 1 2 3 4 start 5 6 8 9 7 ACCEPTED s h e State Machine that recognizes the strings “ he”, “hers”, “his”, and “she”įinite State Machine (DFA) 0 1 3 2 start 4 A DFA that recognizes the strings “ and”, & “any” a n d ACCEPTED yįinite State Machine (DFA) 0 1 3 2 start 4 A DFA that recognizes the strings “ and”, & “any” a n ACCEPTED 1 Accept all strings that end in a 1 q 0 q 1 0 1 1 0 StartĭFA Examples Strings with an odd number of ones. Each state has a transition for every symbol in the alphabet 2ĭFA Examples Example. Parts of a DFA 1 0 1 1 0 accept state transition start state The alphabet for this example is. There is a precise mathematical definition of exactly what is meant by a finite automaton If the input ends and the DFA is in an accept state then the string is 'recognized' A 'language' can be described as a set of strings A language is called a regular language if some finite automaton recognizes it. Upon receipt of a certain symbol, it will go to a known state Finite : The machines only have a certain number of states Automata : Machine, robot ĭFA's DFA's recognize strings. Why study regular expression and DFA?ĭeterministic Finite Automata Theoreticians have developed a number of theoretical models to describe 'computing' Simplest model is known as a DFA Deterministic : Machine will be in a state. Validate data-entry fields (dates, email, URL, credit card). An accepting state is denoted by a double circle. A set of states F called as the accepting states or final states. A state S 0 (sometimes denoted by Q 0 ) called as the start state or initial state. A set of input symbols ∑ (alphabet) A transition function δ that maps state-symbol pairs to sets of states. Nondeterministic Finite Automata A nondeterministic finite automata (NFA) is collection of 5 things or 5 tuple: A set of states S. Tekwani Elphinstone College Mumbai, India 2006 Finite Automata Finite Automata Salomaa, "Formal languages", Acad.Finite Automata Mukesh N. Ginsburg, "The mathematical theory of context-free languages", McGraw-Hill (1966)Ī. Ulman, "Introduction to automata theory, languages and computation", Addison-Wesley (1979) Stearns, "Algebraic structure theory of sequential machines", Prentice-Hall (1966) Ginsburg, "Algebraic theory of automata", Acad. DFA, UFA, and NFA recognize exactly the same class of formal languages. Each deterministic finite automaton (DFA) is an UFA, but not vice versa. Behaviour and synthesis", North-Holland (1973)Ī. In automata theory, an unambiguous finite automaton ( UFA) is a nondeterministic finite automaton (NFA) such that each word has at most one accepting path. It then introduces Pynini, a Python library for compiling finite-state grammars and for.
Gladkii, "Formal grammars and languages", Moscow (1973) (In Russian) This book first provides a detailed introduction to this formalism. The regular languages form a proper subclass of the class of linear languages (cf. The class of languages generated by regular grammars (regular or automatic languages) coincides with the class of regular sets if rules with an empty right-hand side are allowed. To the previous languages.) For each regular grammar it is possible to construct a finite automaton (cf. Is the empty string, are also sometimes allowed the class of languages generated is then extended only at the expense of the languages obtained by adding the string $ \Lambda $ (Rules of the form $ A \rightarrow \Lambda $,
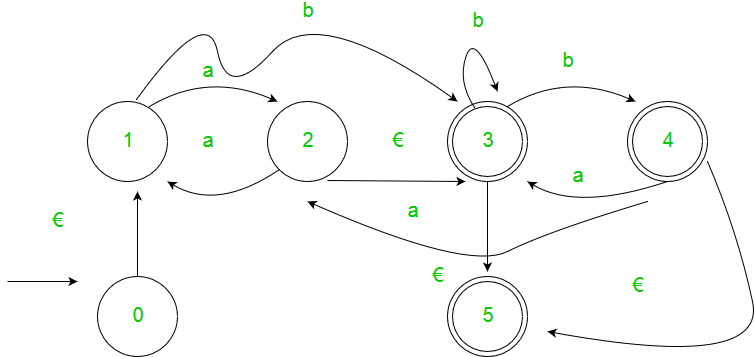
Grammar, context-free) each rule of which has the form $ A \rightarrow aB $ Finite-state grammar, automatic grammar, left- (right-) linear grammarĪ context-free grammar (cf.


 0 kommentar(er)
0 kommentar(er)
